Which of the Following Statements About Convergence of the Series

By Ra_Lilah949 11 Apr, 2022 Post a Comment

CThe series å n1 n sin1 is convergent. If the value received is finite number then the series is converged.

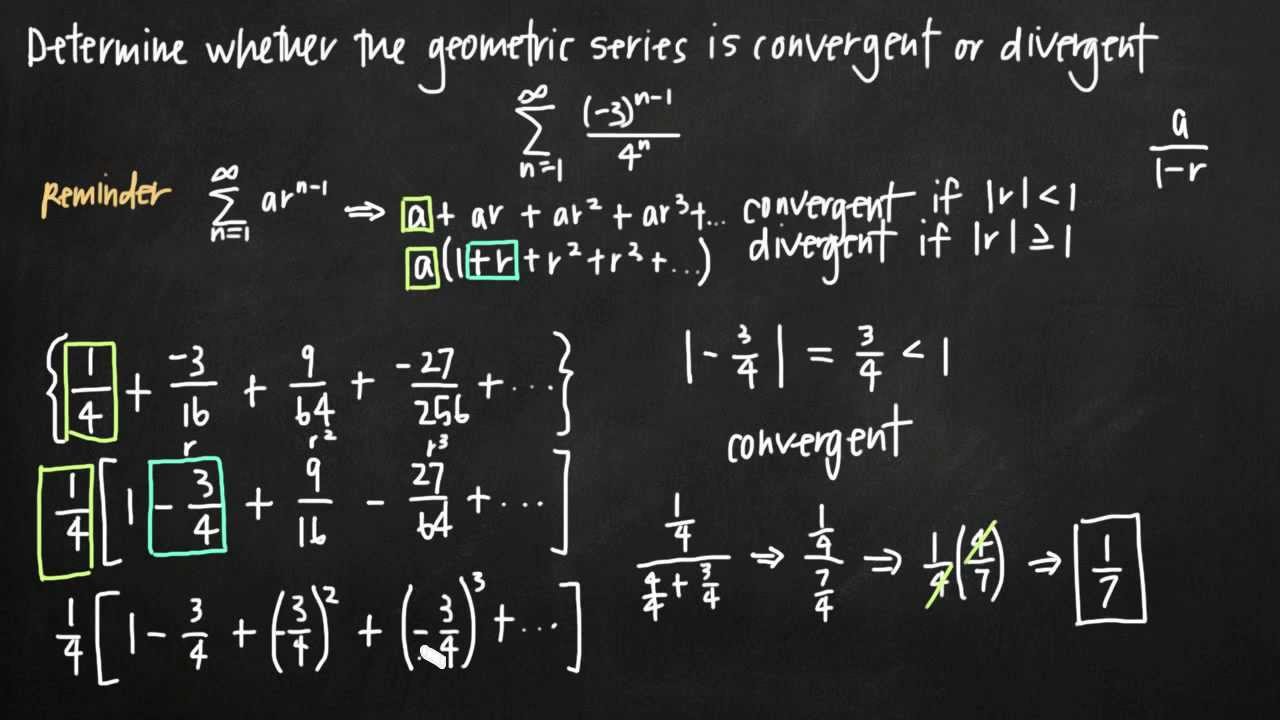
Convergence Of A Geometric Series Kristakingmath Youtube

Which of the following statements about convergence of the series is true.

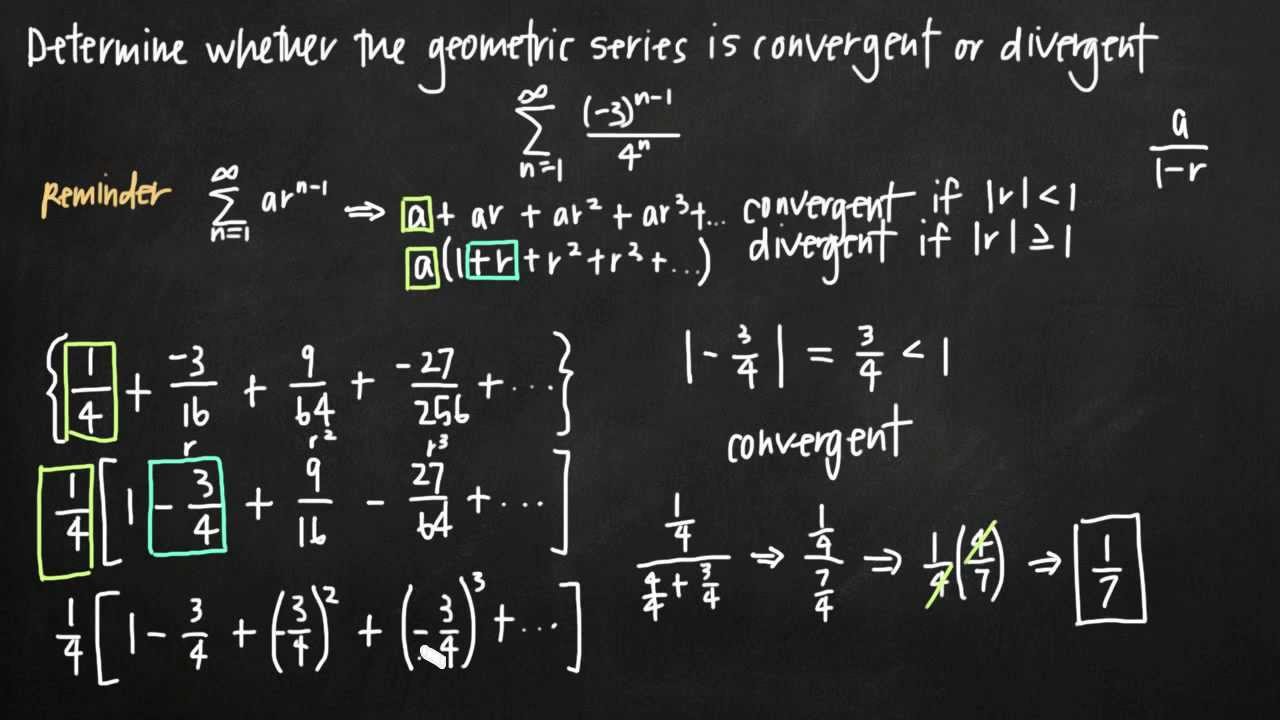
. There is only one AIf 0 bn an and åbn converges then åan converges. Which of the following statements about convergence of the series is true. Solution for Which of the following statements about convergence of the series is true.

A series an a n is said to converge absolutely if an a n also converges. Tests for Convergence Let us determine the convergence or the divergence of a series by comparing it to one whose behavior is already known. A The series converges conditionally at x 6 B The series diverges at x 6 C The series converges absolutely at x 6 D The convergence at x 6 cannot be determined using the given information.

1 point Each of the following statements is an attempt to show that a given series converges or not using the Comparison Test NOT the Limit Comparison Test For each statement enter C for correct if the argument is valid or enter I for incorrect if any part of the argument is flawed. Absolute convergence is stronger than convergence in the sense that a series that is absolutely convergent will also be convergent but a series that is convergent may or. Which of the following statements about convergence of the series 1 In n 1 is true.

Free series convergence calculator - test infinite series for convergence step-by-step This website uses cookies to ensure you get the best experience. Lim n an1 an lim n 1 1 nn x xe. The Cauchy condition The following Cauchy condition for the convergence of series is an immediate con-sequence of the Cauchy condition for the sequence of partial sums.

There are different ways of series convergence testing. 7Which of the following statements is true. Which of the following statements is true regarding the convergence project by the FASB and IASB.

II- The order of convergence isnt linear. The converged framework will be a series of documents similar to the two conceptual frameworks that presently exist. 1 Which of the following statements about convergence of the series is true.

For all n 2 ln nn 1n and the series 1n diverges so by the Comparison Test the series ln nn diverges. EThe ratio test can be used to show that å 1 n10 converges. Without such assumption you may consider examples such as a_n-1n.

The second statement is equivalent to the convergence of the sum in mathbbR mathbbRn mathbbCn or any complete normed space you name it. By using this website you agree to our Cookie Policy. β lim sup a n 1 n R 1 β.

As an asymptotic series but we wont discuss them further here. This series is converged. III- The asymptotic rate of convergence is 05 O I and II O I II and II O I and II O Il and III.

We can see that. 2 nInn1 A 2 converges by comparison with Σ n-1Inn 1 n-1 Σ B converges by comparison with L In n 1 2 Σ C diverges by comparison with 1n D X In I diverges by comparison with -1 Inn 1 n Question. For x 1 e we have.

N1 hein Β Σ 1 In n 1 -converges by comparison with 2 n1 n1n 00 1 C Σ. The series P 1 n1 1 2 converges so the comparison test tells us that the series P 1 n1 2 also converges. N1 In n 1 1 Α Σ - converges by comparison with 2- n1 In n 1 n1 1 Β Σ n1 In n1 - converges by comparison with.

N1 nal 00 1 D Σ diverges by comparison with In n 1 2 n1. We want to find the the radius of convergence and exact interval of convergence for the series. Let a n e nn2.

2 The divergence of P1 n1 an implies the. For instance because of. Begingroup The first statement is equivalent if a_n are assumed to be non-negative reals.

Since e n. The series P 1 n1 1 2 converges so the comparison test tells us that the series P 1 n1 e n n2 also converges. The series X1 n1 a n converges if and only for every 0 there exists.

An 1 n. BIf lim n an 0 then the series åan is convergent. Theorem 48 Cauchy condition.

It follows that the series is convergent for x 1 e and divergent for x 1 e. P 1 n1 1 2 converges so P 1 n1 e n converges. 1 C Σ diverges by comparison with 2 In n 1 n1 1 D Σ diverges by comparison with n1 In n 1 n1n.

Calculus questions and answers. In n1 diverges by comparison with 9. Which of the following statements about the convergence of the series at x 6is true.

First of all one can just find series sum. Which of the following statements is True regarding the convergence of the bisection method. For all n 1 arctan nn³ π2n³ and the series π2 1n³ converges so by the Comparison Test the series arctan nn³ converges.

Comparison test Suppose 0 an bn for n k for some k. Inn1 1 A converges by comparison with Inn 1 1 00 B 2 Inn1. DIf åan is convergent for an 0 then å 1nan is also convergent.

Then 1 The convergence of P1 n1 bn implies the convergence of P1 n1 an. Betalimsup lefta_ nright frac 1 nhspace 2mm. I-The iteration is always guaranteed to converge.

N1 00 Α Σ 1 In n1 converges by comparison with 2. If we wasnt able to find series sum than one should use different methods for testing series convergence.

Alternating Series Test Question Mathematics Stack Exchange